Morse code is a method of transmitting textual information as a series of on-off tones, lights or clicks that can be directly understood by a skilled listener or observer without special equipment. The International Morse Code encodes the Roman alphabet, the Arabic numerals and a small set of punctuation and procedural signals as standardized sequences of short and long "dots" and "dashes", or "dits" and "dahs". Because many non-English natural languages use more than the 26 Roman letters, extensions to the Morse alphabet exist for those languages.

A related but different code was originally created for Samuel F. B. Morse's electric telegraph in the early 1840s. In the 1890s it began to be extensively used for early radio communication before it was possible to transmit voice. In the early part of the twentieth century, most high-speed international communication used Morse code on telegraph lines, undersea cables and radio circuits. International Morse code today is most popular among amateur radio operators, where it is used as the pattern to key a transmitter on and off in the radio communications mode commonly referred to as "continuous wave" or "CW". Other keying methods are available in radiotelegraphy, such as frequency shift keying.
Time structure
The basic element of Morse code is the dot and all other elements can be defined in terms of multiples of the dot length. The other elements are dash (= dot length x 3), pause between elements (= dot length), pause between characters (= dot length x 3) and pause between words (= dot length x 7). An example is the word PARIS that has length of 50 dot lengths:

Words Per Minute
The word PARIS (shown above) is used as standard of the typical word in English plain text. Morse code speed is specified in words per minute (WPM). This means that if we transmit the word PARIS (that has length 50 dot lengths) in 1 minute then the speed is 1 WPM. Also if we send PARIS (or any other word 50 dot lengths long) ten times in a minute then the code speed is 10 WPM. In case of 1 WPM the duration of a dot is 60 seconds / 50 dots per minute = 1.2 seconds per dot. Also in any other speed we can define the dot length as equal to 1.2 seconds divided by the speed in WPM. Based on the above we can use the following formulas:
or
Dot length (Seconds) = 1.2 / Speed (WPM)
Bandwidth
A CW signal of 12 WPM means 12x50 = 600 dot lengths per minute or 600/60 = 10 dot lengths per second. Since pause between elements (dots or dashes) is equal to dot length, if a continuous series of dots is given at 12WPM this results in a 10/2 = 5 Hz square wave. If an RF signal is keyed with this series of dots we will get a carrier with 2 sidebands at 5Hz, resulting in a 10Hz wide signal.
This result based on a fundamental principle of trigonometry, that says that modulating a sine wave with another sine wave (which is actually multiplying the two waveforms) yields 2 signals, one at the sum of the frequencies and the other at the difference of the frequencies. This assumption is based on the case where the keying is not "hard" (rapid on-off) but with additional RC circuits we shape the square keying waveform to look like sine and have gradual (and not rapid) turn on/off. In real world "hard" keying is never used because the modulation of a carrier with a square wave is a disaster. It is known that a square wave is composed of an infinite number of harmonics and probably at least the first 30 or so are significant, so using hard keying means modulating a high frequency carrier sine wave with a low frequency square wave and the result will be a very wide frequency spectrum with a lot of sidebands that are waste of energy and production of interference.
Above we saw that a 12 WPM baseband signal produces a 10Hz wide RF signal and this leads to a ratio of 12/10 = 0.833. Concluding, we can say that the minimum bandwidth that is required to receive a CW signal undistorted is:
Signal to Noise Ratio
Signal-to-noise ratio (often abbreviated SNR or S/N) is a measure used in science and engineering to quantify how much a signal has been corrupted by noise. It is defined as the ratio of signal power to the noise power corrupting the signal. A ratio higher than 1:1 indicates more signal than noise. In less technical terms, signal-to-noise ratio compares the level of a desired signal to the level of background noise. The higher the ratio, the less obtrusive the background noise is. Signal-to-noise ratio is defined as the power ratio between a signal (meaningful information) and the background noise (unwanted signal):
where P is average power. Both signal and noise power must be measured at the same or equivalent points in a system, and within the same system bandwidth. Because many signals have a very wide dynamic range, SNRs are often expressed using the logarithmic decibel scale. In decibels, the SNR is defined as:
It is very easy to understand that in a receiver that gets CW signals, higher SNRs lead to higher possibilities for correct detections and decodes of the Morse code messages. A typical radio link consists from the transmitter, transmission line, transmitting antenna, air path, receiving antenna, reception line and the receiver. In order to calculate the SNR we need a LOT of information that range from "known" values such as the transmitting power, losses in transmission and reception lines, gains of transmission and reception antennas, signal bandwidth to other more complex and maybe completely unknown values like noise figure of the receiver and loss of the air path that depends from distance (that the airwave crossed) which most of the times is completely unknown and especially in HF bands where the airwave gets reflected by the ionosphere and we don’t know the number of hops nor if it was traveled via the short or the long path between the two locations.
If we want to improve the SNR we can do it by change one or more of the factors that affect SNR. We may increase SNR by increase the transmit power or the receive/ transmit antenna gains or decrease transmission/reception line losses but all these require changes in the equipment that is not always possible. We can also increase SNR by decrease the bandwidth. Why? A wider bandwidth includes more noise, so reducing receiver’s bandwidth will always increase SNR. In the previous section we saw that the bandwidth occupied by a CW signal depends from the Morse code speed in WPM and if we decrease the code speed in WPM then the bandwidth decreases.
All these mean that we may not be able to calculate the SNR accurately or not calculate it at all BUT we can calculate the improvement of the SNR (dB) of a lower code speed (WPM) against a higher code speed (WPM). In a few words this means that if we have established a communication link with e.g. 12 WPM and 10W of transmitting power if we reduce the code speed to 4 WPM we will have an improvement on SNR several dBs BUT since the SNR of 12 WPM was enough for correct decoding of Morse code messages we can decrease the transmitting power of the 4 WPM transmission the same amount of dBs (as the improvement on SNR from 12 WPM to 4 WPM) and achieve on 4 WPM the same SNR with 12 WPM (that is enough to decode correct). The conclusion here is that we can achieve CW communication by lowering the transmitting power (W) if we lowering also the code speed (WPM).
From all previous formulas we can calculate the improvement of SNR in dBs of the previous example. The bandwidth of 12 WPM is 0.833x12 = 10 Hz also the bandwidth of 4 WPM is 0.833x4 = 3.333 Hz. So the improvement of the SNR (dB) from the 12 WPM to 4 WPM is SNR (dB) = 10xlog10 (BW of 12 WPM / BW of 4 WPM) = 10xlog10 (10/3.333) = 10x0.477 = 4.77 dB. This means that we can reduce the transmitting power of 10W that it was used on 12 WPM by 4.77 dB and achieve exactly the same SNR on 4 WPM. To become more precise 10 W = 40 dBm by decreasing it 4.77 dB it becomes 40-4.77 = 35.23 dBm BUT 35.23 dBm = 3.33W. Nice ha? by reducing the code speed from 12 WPM to 4 WPM we can have the same SNR by using instead of 10 Watts only 3.33 Watts (66.6% less power)!!!
Based on the fact that the majority of CW communications within HF bands take place in code speeds around 20 WPM, I used this code speed as reference and calculated the improvement in SNR (dB) for lower code speeds that go down to 600 seconds per dot (0.002 WPM):
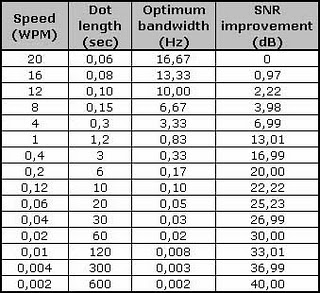
Conclusions: Studying carefully the above table we can see that the more slower we send the more lower transmitting power we need. In my experience it is possible to have CW communications (QSOs) on 20 WPM with QRPp power lower than 1W. This means that if we reduce the speed extremely slow to 0.002 WPM (10 mins per dot) we can achieve the same distance with 40 dB lower than 1W. How much is it? It is only 100 uW (microwatts). W-O-W !!!!!!
References:
[1] Wikipedia, Morse code, http://en.wikipedia.org/wiki/Morse_code
[2] Nu-Ware, Morse code structure and timing, http://www.nu-ware.com/NuCode%20Help/index.html?morse_code_structure_and_timing_.htm
[3] ON7YD, Extreme narrow bandwidth techniques, http://www.qsl.net/on7yd/136narro.htm
[4] W5ALT, CW Bandwidth, http://www.comportco.com/~w5alt/cw/cwindex.php?pg=5
[5] Wikipedia, Signal-to-noise ratio, http://en.wikipedia.org/wiki/Signal-to-noise_ratio